声明:“工程应用常见问题案例解析”专栏是通过工程案例来阐释软件应用的常见问题以及解决办法的,我们希望能给遇到类似问题的工程师提供一些参考。本栏目里的所有案例都来源于筑信达软件的用户,软件模型归属于设计单位,相关的内容只是用于软件应用技术方面的探讨。如果有不妥之处,请联系我们将其删除。
钢结构网壳的双非线性稳定性分析
本文以某双层钢结构网壳作为例子,主要介绍了非线性参数对双非线性稳定性分析的收敛性以及“荷载 - 位移”曲线的影响,同时也介绍了塑性铰覆盖项对这些方面的影响。
1.使用软件
SAP2000中文版 v26.0.1
2.模型简介

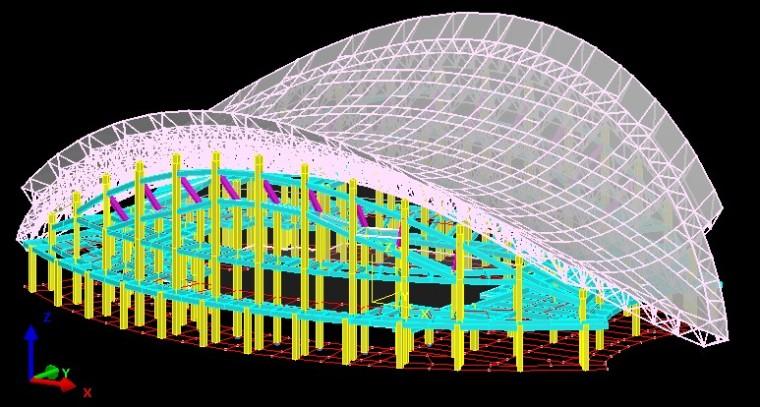
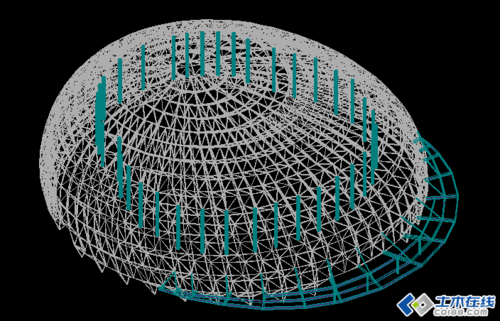
该双层钢结构网壳如图 1 所示,它由不同尺寸的圆钢管构成。集中力形式的恒载和活载通过以虚面定义的蒙皮来传递,其中恒载包含结构自重以及屋面恒载 0.25kN/m²钢结构网,活载为 0.5kN/m²。
为完成结构的双非线性稳定性分析,首先要在全部圆钢管的跨中位置处指定轴力铰。接着,以特征值屈曲分析的第一阶屈曲模态来引入结构的整体几何缺陷。最后,在非线性静力分析中需考虑“P-Delta 以及大位移”效应,并且通过监测点位移来控制加载过程。
图1 双层钢结构网壳的计算模型
3.问题描述
该模型的双非线性稳定性分析无法收敛。从图中可以看出,出铰位置较少(如左图所示)。并且,“荷载 - 位移”曲线基本为直线(如右图所示)。由于这种情况,无法获取理想的极限荷载和曲线下降段。
图2 初始的塑性铰分布和“荷载-位移”曲线
4.解决办法
以上非线性分析的收敛问题与塑性铰强度损失(负刚度)所引发的弹性回弹存在关联。塑性铰强度损失会导致弹性回弹,而弹性回弹产生的卸载变形与塑性变形的符号不同,并且其大小远超过塑性变形,这对非线性分析的收敛性和计算精度产生了严重影响。然而,弹性回弹并不符合钢结构实际的受力状态,同时也不是结构工程师所关注的重点内容。
为减小因塑性铰强度损失而导致的收敛性问题,建议降低塑性铰在卸载阶段的负刚度值钢结构网,这样就能避免出现弹性回弹。从图 3 可以看出,选中全部构件后,把框架铰覆盖项的负刚度比例修改为 0.01(原本的默认值是 0.1)。此比例表示塑性铰强度损失的负刚度与构件弹性刚度的比值,该比值越小,卸载就越缓慢,也就越不容易发生弹性回弹。
图3 修改塑性铰卸载的负刚度比例
图4 修改非线性求解策略

考虑塑性铰的非线性静力分析或者非线性直接积分法的时程分析时,ETE(Event to Event 事件到事件)求解策略通常能够改善非线性分析的收敛性。然而,倘若模型中包含众多塑性铰或者考虑其他类型的非线性,将 ETE 关闭往往能够提升计算效率。本文的双层钢结构网壳为例,这个模型包含近 5000 个塑性铰,同时还考虑了 P-Delta 和大位移效应。所以,建议关闭 ETE 并采用“仅迭代(Iterative only)”的求解策略,就像图 4 所展示的那样。
完成上述两个操作之后,不但能够大幅提升计算效率,还能够顺利地完成结构的双非线性稳定性分析。从图 5 能够看出,修改后的出铰位置增多了,塑性铰的分布范围也变大了,这与预期相符。
图5 修改后的塑性铰分布
如图 6 所示,对比三个计算模型的“荷载 - 位移”曲线后可以发现:仅考虑几何非线性时,结构的极限荷载是 109;仅考虑材料非线性时,结构的极限荷载为 8.2,比仅考虑几何非线性时的极限荷载小很多;同时考虑材料和几何非线性时,结构的极限荷载为 8.0,略微小于仅考虑材料非线性时的极限荷载,这与预期相符。
图6 理想的“荷载-位移”曲线
编撰|张志国
排版|王蓉
审核|李立








